E-Graph
E-Graph는 Equivalence Relation (동등 관계)를 표현하는 자료구조 이다. 이는 어떠한 두 원소가 같다라는 것을 보일 때 효과적인 자료 구조이다. 최근에는 PL 학계에서도 많은 관심을 가져 EGRAPHS 워크숍도 꾸준히 진행되고 있다. 최근에는 이 E-graph를 활용하여 컴파일러 최적화를 더 똑똑하게 하려는 연구가 많이 진행되고 있으며 Wasm 엔진 Wasmtime의 JIT-Compiler인 Cranelift에서도 이런 E-graph를 활용하고 있다. 이 cranelift에 대한 설명은 다음 글에서 설명할 예정이다.
E-Graph로 프로그램 표현하기
e-graph로 프로그램을 표현하게 되면 각 노드 (e-node)는 그 노드가 root node인 sub expression을 나타내게 된다.
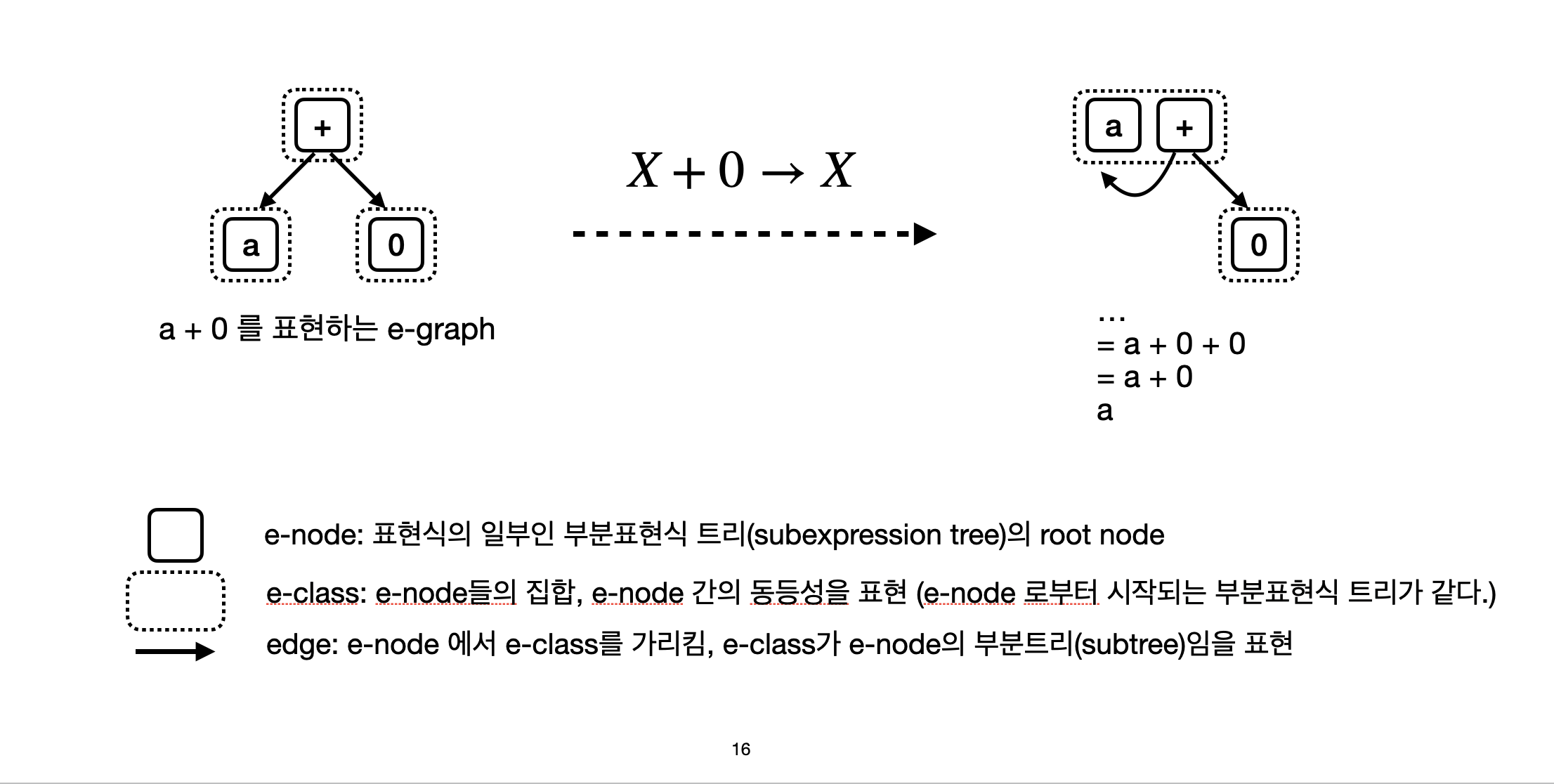
a + 0 이라는 프로그램을 나타내게 되면 + 노드는 a + 0을 나타내고, a노드는 a라는 프로그램을 나타내게 된다. 그리고 동등성을 표현하는 점선으로 묶인 e-class는 e-node들을 묶으며, 묶인 e-node가 동등하다라는 것을 표현한다.
만약 a + 0 과 a라는 프로그램이 같다라는 것을 표현하고자 한다면 아래 그림의 오른쪽 그래프처럼 a와 +가 e-class로 묶여서 나타나게 된다. 이렇게 e-graph로 프로그램의 동등성을 나타내게 된다. 일반적인 컴파일러 최적화에서 최적화는 프로그램을 최적화된 프로그램으로 rewrite 하는 rewrite rule 형식으로 작성되기 때문에, e-graph를 컴파일러에 적용하려는 노력이 이어지고 있다.
E-graph를 통한 컴파일러 최적화
E-graph는 위에서 설명한 것처럼, 최적화 전 프로그램을 e-graph로 표현하고, rewrite rule 형식으로 최적화를 모두 적용한 다음 가장 비용이 적은 프로그램을 선택하면 최적화가 되는 구조로 되어있다. 실제 예시로 보자 아래와 같은 최적화 전 프로그램이 있다고 하자.
int foo(int a) {
return (a*2)/2;
}
그러면 이 프로그램은 아래와 같이 표현될 것이다.
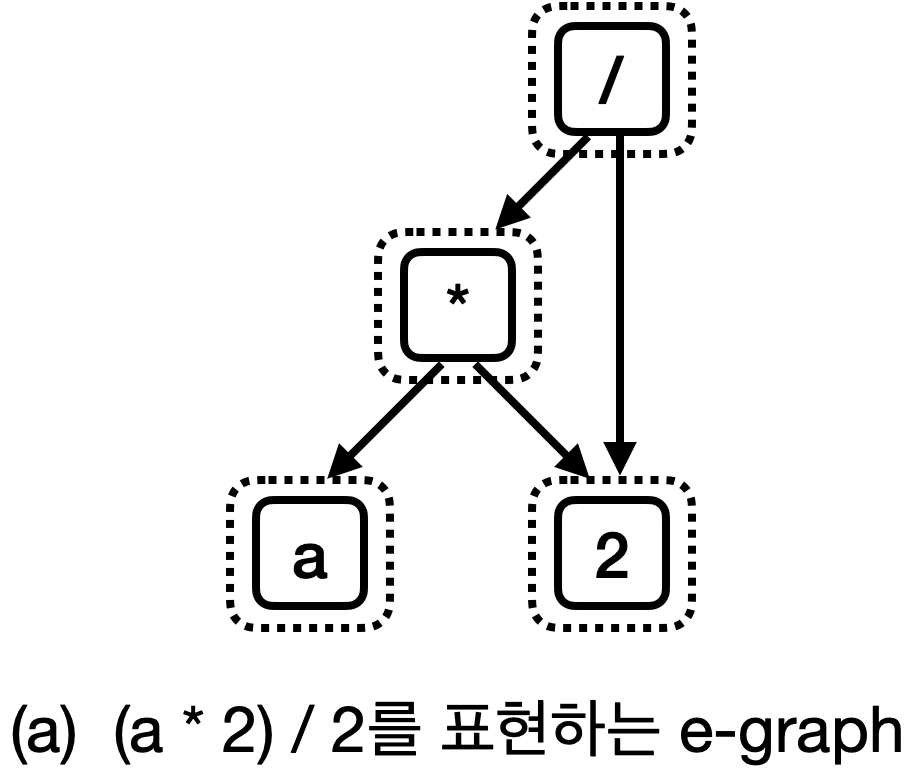
그렇다면 이제 컴파일러에 존재하는 최적화 중, 적용될 수 있는 것들을 하나씩 적용하면서 e-graph를 업데이트한다. 만약 (X * Y) / Z -> X * (Y / Z) 라는 재작성 규칙을 표현하면 아래와 같을 것이다.
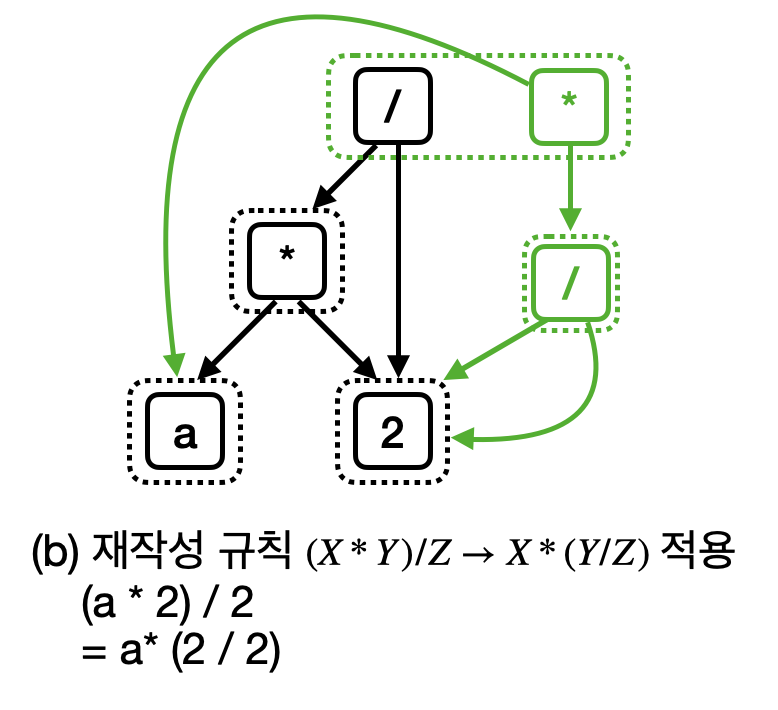
만약 X / X -> 1, X * 1 -> X 까지 모두 적용 하면 아래와 같게 될 것이다.
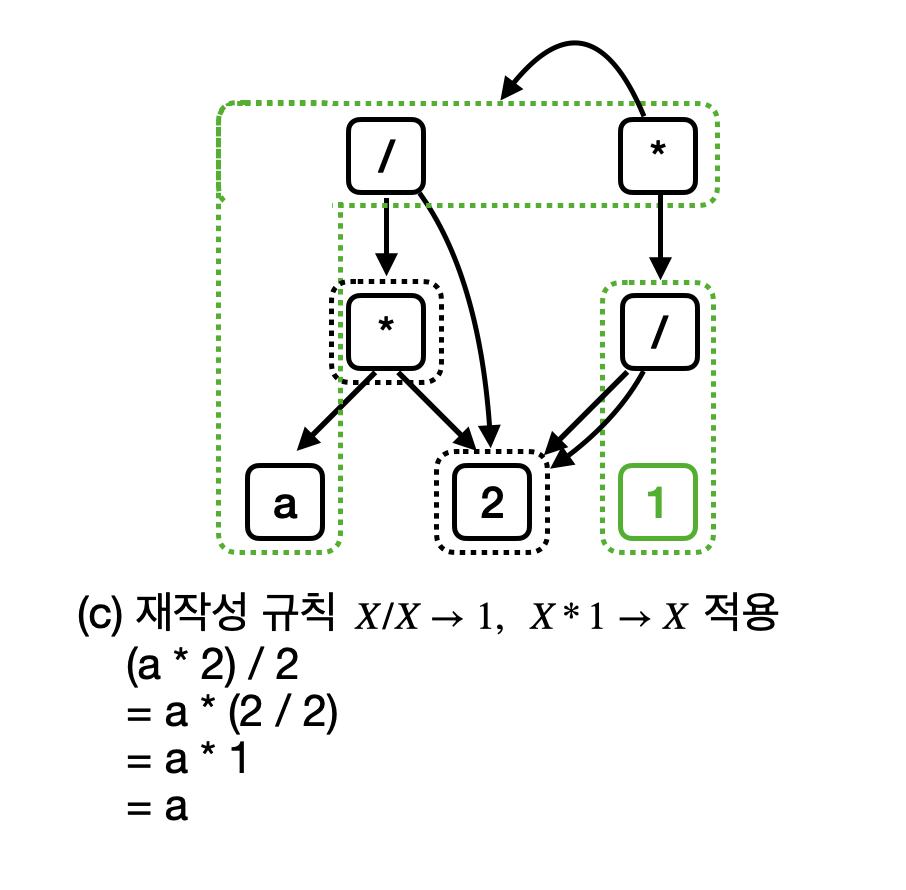
최종 E-graph를 해석해보면 (a * 2) / 2 , a * (2 / 2), a * 1, a 라는 프로그램이 모두 같게 된다. 그 중 가장 비용이 적은 a라는 프로그램을 선택하면 최적화된 프로그램은 결국 아래처럼 return a; 가 된다.
int foo(int a) {
return a;
}
E-graph를 통해 컴파일러 최적화를 구현하면 장점은 다음과 같다.
- E-graph 자료구조를 통해 프로그램 최적화 과정을 간결하게 (compactly) 표현할 수 있다.
- 최적화 규칙이 재작성 규칙(rewrite rule)으로 주어졌을 때, 정확하게 최적화를 표현할 수 있다.
- 해당 최적화 프레임워크를 구축한다면, 여러 컴파일러에 쉽게 적용이 가능하다.
아직 실제 복잡한 현대 컴파일러들에 바로 적용되기에는 해결해야 하는 문제들이 존재하지만 e-graphs를 최적화 일부에 적용하는 것은 지금도 가능하고, 많은 사람들이 시도하려는 문제이다.