컴파일러 최적화 증명하기
최근 컴파일러의 최적화를 일반화(generalize)하고, 다른 컴파일러에 이식(transplantation)을 하는 연구를 시작하면서 자연스럽게 최적화를 자동으로 증명하는 법을 연구하게 되었다.
최적화를 일반화 하기위해서는 해당 최적화가 어느 타입에까지 올바른 최적화인지를 알아야 하기 때문이다.
예를 들어, (X + 1) + 2 -> X + 3 이라는 최적화는 (X + C1) + C2 -> X + (C1 + C2) 라는 최적화로 일반화를 할 수 있을 것이다.
이런 경우에는 (X + C1) + C2 -> X + (C1 + C2) 라는 최적화가 올바르다는 것을 증명해야만 우리의 일반화가 올바르다고 말할 수 있을 것이다.
LLVM의 경우 최적화가 몇 천개가 넘게 존재하기 때문에 이를 모두 손으로 증명하는 것은 불가능하기 때문에, 자동으로 증명을 해야 한다.
다행히 같이 AWS에 계시는 이준영 박사님, John R Harris 박사님의 도움을 받아 LLVM의 최적화를 자동으로 증명을 하는 법에 크게 도움을 받았다.
HOL Light이라는 interactive theorem prover를 사용하여 증명을 하는 것이다.
당연히 interactive theorem prover이기 때문에 기본적으로 사람이 수동으로 구현을 해야하지만, 박사님들의 도움으로 자동으로 증명하는 tactic을 구현하고, 이를 통해서 자동으로 증명하는 법을 만들어냈다.
HOL Light를 기본적으로 사용하는 법은 이준영 박사님이 정리해주신 깃헙이 있어서 편하게 사용할 수 있다.
이 글에서는 기본적으로 수동으로 최적화를 증명해보고, 후에 자동으로 최적화를 증명하는 법도 정리해보자 한다.
수동으로 최적화 증명하기
LLVM의 최적화를 생각해보면 모든 값을 비트단위에서 생각해야 한다. 만약 X + Y -> X | Y if X, Y has no common bits 라는 최적화를 생각해보면 bitwise or 연산을 생각해야 하기 때문에 X, Y 모두 정해진 길이의 비트 스트림으로 생각해야한다.
HOL Light에서 이런 것을 다룰 수 있는 것이 WORD tactic이다.
이제 제일 간단한 2개를 증명해 보려고 한다. 첫 번 째는 (X + C1) + C2 -> X + (C1 + C2) 이다.
임의의 N bit의 정수들이라고 할 때, 아래처럼 우리가 증명할 수식을 적을 수 있다.
g `!(x:(N)word) c1 c2. (word_add (word_add x (word c1)) (word c2)) = (word_add x (word (c1+c2))) `;;
g는 우리가 증명할 목표(goal)을 의미하고, !는 forall을 의미한다.
위와 같은 간단한 목표는 HOL-Light에 기본적으로 내장된 WORD Rule들을 이용하여 증명할 수 있다. 기본적으로 내장된 룰은 아래 처럼 검색해볼 수 있다.

그렇다면 기본적으로 결합법칙을 설명하는 공리들을 발견할 수 있기에, 이러한 공리들을 조합하여 증명을 할 수 있을 것이다. 아니면, 자동으로 공리들을 조합해주는 tactic을 써볼 수도 있을 것이다.
e(CONV_TAC WORD_RULE);;
자동으로 최적화 증명하기
위에 언급한 것처럼, 이미 HOL Light에 기존 공리들을 조합하는 기능이 있긴 하지만 이를 통해서 컴파일러에 존재하는 실제 최적화들을 자동으로 증명하는 것은 불가능하다. 기본 탑재된 공리도 부족하기에 그런 공리들을 사람들이 넣어주기 어렵고, 복잡한 최적화를 증명하기에는 성능이 안좋기 때문이다.
그렇기에 우리는 새로운 방법을 고안해야 했다. 이 때, Harris 박사님께서 큰 도움을 주셔서 Bit Blasting으로 증명을 하는 법이 탄생하게 되었다.
Bit Blasting은 주어진 비트벡터 논리식(Formula)에 대해서 비트 단위로 증명하는 기법이다.
아래는 Bit Blasting의 예시이다.

그렇다면 이 것을 이용해서 최적화를 어떻게 증명할까? 가장 간단한 최적화인 X + 0 -> X 최적화를 증명해보자.
(마크 다운으로 작성하기 불편해서 키노트로 그려보았다)
우리의 증명목표는 아래와 같을 것이다.

이 때, 귀납적으로 증명하기 위해서 i + 1 번 째 비트와, i 번 째 비트의 관계를 계산한다. 이 경우에는 덧셈을 증명하기 때문에 최대 1개의 비트가 carry가 될 수 있기 때문에 add를 인코딩하여서 아래와 같이 쓸 수 있다.

이를 귀납적으로 작성하면 아래와 같이 표현할 수 있다. 우리의 목표는 X + 0과 X 가 모든 비트가 같다라는 것을 증명하고 싶기 때문에,
X + 0의 0 번째 비트와 X의 0번째 비트가 같고, X + 0 의 i번째 비트와 X의 i 번째 비트가 같을 때, X + 0의 i+1번 째 비트와 X의 i+1 번째 비트도 같다라는 것을 보이면 최적화를 증명할 수 있다.
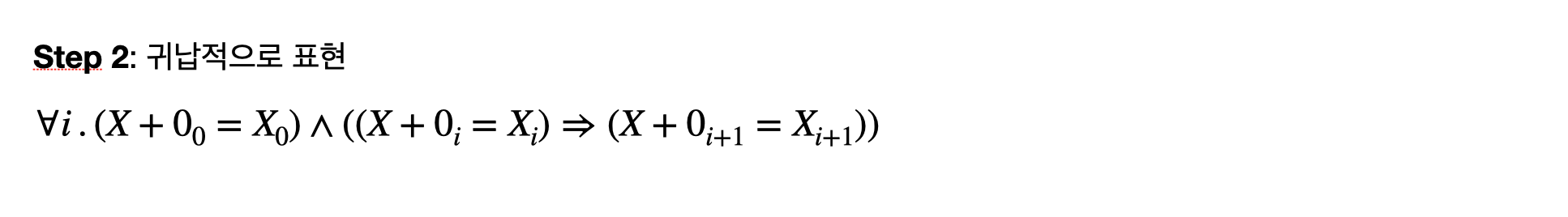
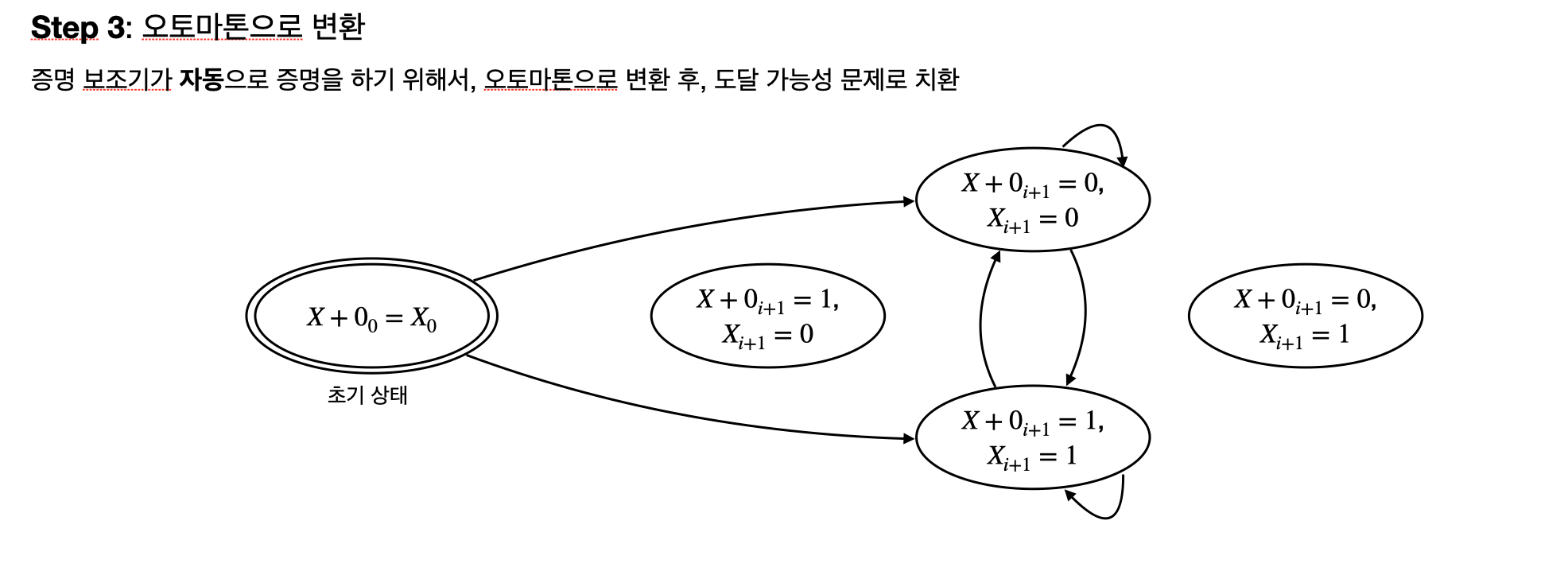
이렇게 표현을 했으면 이는 오토마톤으로 그리면 아래와 같이 그릴 수 있다. 이는 HOL Light가 자동으로 증명하기 위해 아래와 같은 오토마톤으로 표현한 뒤, 도달 가능성 문제로 치환해서 증명할 수 있다. X + 0과 X의 0번째 비트가 같다라는 시작 상태에서 도달할 수 있는 모든 상태에서 X + 0과 X가 같다라면 이는 우리가 최적화를 증명한 것이다.
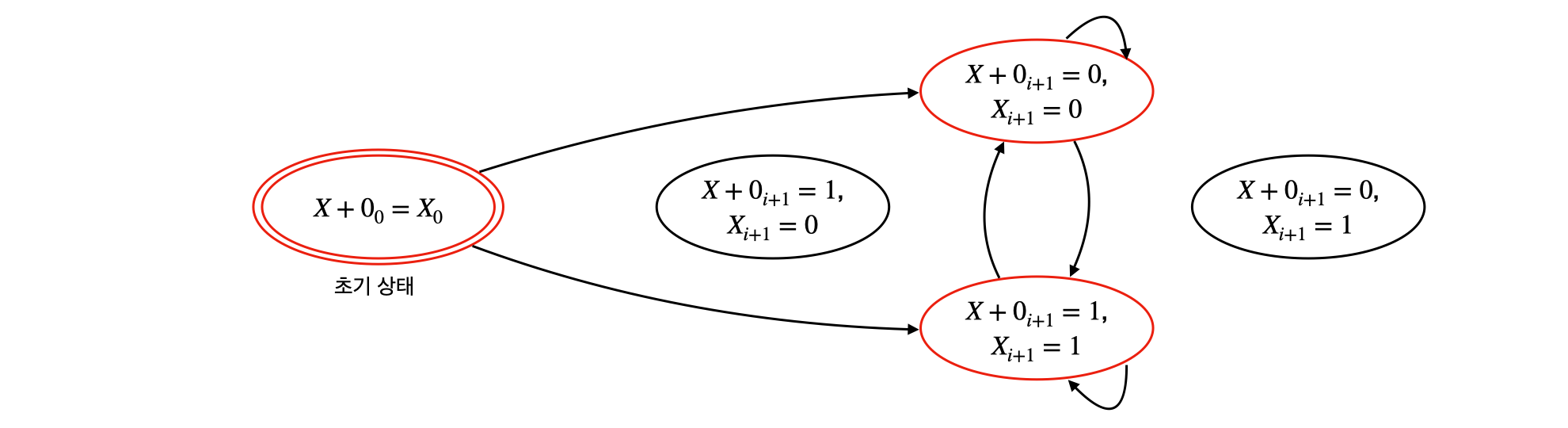
실제로 도달가능한 모든 state는 비트가 같기 때문에 X + 0 -> X 최적화는 모든 비트 크기의 정수 타입에서 올바르다라는 것이 증명된다.
여담
처음에는 기존 컴파일러 최적화를 새로 생겨나는 컴파일러에 최적화를 이식하기 위한 연구에서, 최적화를 증명하는 것은 아주 작은 문제일 줄 알았으나, 일이 이렇게 커질 줄은 상상도 하지 못했다. 혼자라면 이 문제를 전혀 풀지 못했겠지만, 이 문제를 위해 박사 3분이 나를 도와주셔서 최적화를 자동으로 증명할 수 있게 되었다. 물론 현재 우리의 방법이 세상에 존재하는 모든 최적화를 자동으로 증명하지는 못하지만, 현재 PLDI 2015에 투고되었던 논문에서 증명한 최적화의 거의 대부분을 우리가 모든 비트 타입에 대해서 올바르다는 것을 증명할 수 있었다. 또한 Harris 박사님께서 Proof Systems for Mathematics and Verification에서 우리의 일을 발표에서 언급해주시면서 우리가 한 일이 어떤 의미를 가졌는지를 여러 사람들에게 알려주셨다. 워크숍 영상
